
|
Tools - Math 'Convincing and Proving' Critiquing 'Proofs' Tasks, Set #3 (solutions)
Always, Sometimes or Never True: Set #1 (solutions) || Set #2 (solutions)
Critiquing 'Proofs': Set #3 (solutions) || Set #4 (solutions)
Malcolm Swan
Mathematics Education
University of Nottingham
Malcolm.Swan@nottingham.ac.uk
Jim Ridgway
School of Education
University of Durham
Jim.Ridgway@durham.ac.uk
The aim of this assessment is to provide the opportunity for you to:
- evaluate 'proofs' of given statements and identify which are correct;
- identify errors in 'proofs'.
1. Consecutive Addends
Here are three attempts at proving the following statement:
When you add add three consecutive numbers, your answer is always a multiple of three.
Look carefully at each attempt. Which is the best 'proof'? Explain your reasoning as fully as possible.
|
Attempt 1:
|
1 + 2 + 3 = 6
|
3 x 2 = 6
|
|
2 + 3 + 4 = 9
|
3 x 3 = 9
|
|
3 + 4 + 5 = 12
|
3 x 4 = 12
|
|
4 + 5 + 6 = 15
|
3 x 5 = 15
|
|
5 + 6 + 7 = 18
|
3 x 6 = 18 |
And so on.
So it must be true.
|
Attempt 2:
3 + 4 + 5
The two outside numbers (3 and 5) add up to give twice the middle number (4). So all three numbers add to give three times the middle number.
So it must be true.
|
Attempt 3:
Let the numbers be:
n, n + 1 and n + 2
Since
n + n + 1 + n + 2 = 3n + 3 = 3(n + 1)
It is clearly true.
|
The best proof is attempt number ..........
This is because .......
My criticisms of the others are...........
Sample Solution:
Attempt 1 shows that the statement is true for a finite number of cases. The pattern suggests that the result is always true, but this does not constitute a proof.
Attempt 2 is more structural, but again is only related to a specific case.
Attempt 3 is the best attempt at a proof.
2. Areas and Perimeters
Here are three attempts at proving the following statement:
If you have two rectangles, the one with the greater perimeter will have the greater area.
Which is the best 'proof'? Explain your reasoning as fully as possible.
|
Attempt 1:
Suppose you have a rectangle with sides of length a and b.
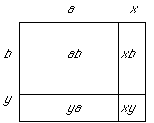 If you increase the perimeter of the rectangle, you must increase these sides.
If you increase the perimeter of the rectangle, you must increase these sides.
Suppose you increase the sides to lengths
a + x and b + y, where x, y ≥ 0
(At least one of x or y >0 or you do not increase the perimeter).
The area obtained will be given by
(a + x)(b + y) = ab + xb + ya + xy > ab
This is clearly greater than the area ab.
So increasing the perimeter must increase the area.
So the statement is true.
|
|
Attempt 2:
Here are some examples:
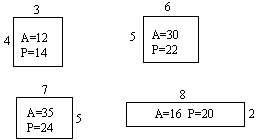
If you put them in a table it is easy to see that the bigger the perimeter, the bigger the area.
|
Perimeter (units) |
14 |
16 |
22 |
24 |
|
Area (square units) |
12 |
20 |
30 |
35 |
So the statement is true.
|
|
Attempt 3:
Just look at these:
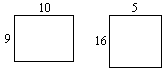
So the statement is clearly false.
|
The best proof is attempt number ..........
This is because .......
My criticisms of the others are...........
Sample Solution:
The statement given here is false.
Attempt 3 gives a counterexample and therefore is the only correct solution - although the perimeter and area are not calculated.
Attempt 1 is flawed in that you can increase the perimeter without increasing both of the sides of the rectangle. Indeed, you can decrease one side and still increase the perimeter. Thus we might have x > 0 and y < 0 so long as x + y > 0.
Attempt 2 clearly only demonstrates the result for a few special cases.
3. Coin Turning
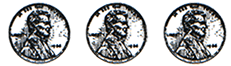
A student is playing a coin turning game. She starts with three heads showing and then turns them over, two at a time.
After a while she makes the statement:
If I turn them two at a time, it is impossible to get all three showing tails.
Here are three attempts to prove this. Look carefully at each attempt. Which is the best 'proof'? Explain your reasoning as fully as possible.
|
Attempt 1:
You can only get the following four arrangements when you turn two at a time:
HHH
HTT
TTH
THT
So it is impossible.
|
Attempt 2:
I will score each position.
Let H = 1 and T = 0. So:
HHH = 1+1+1 = 3,
HTH = 1+0+1 = 2
and so on.
My first position scores 3.
Each time I move, my score will either increase or decrease by 2 or stay the same.
So I can only get into positions with odd scores.
So it is impossible to get a score of zero.
So TTT is impossible.
|
Attempt 3:
It is impossible because the most tails you can have showing is two. When you turn the head over from that position, you must also turn over one of the tails, so you can't get rid of all the heads whatever you do.
|
The best proof is attempt number ..........
This is because .......
My criticisms of the others are...........
Sample Solution:
Attempt 1 shows correct reasoning, but there is no convincing proof that these are the only four positions one can make. There may be others the student has simply not thought of.
Attempt 2 is correct.
Attempt 3 simply explains that it is impossible to reach three tails from a position showing two tails and one head. This is insufficient. (It does not take into account other positions from which one can reach three tails, such as HHT, for example).
Always, Sometimes or Never True: Set #1 (solutions) || Set #2 (solutions)
Critiquing 'Proofs': Set #3 (solutions) || Set #4 (solutions)

|
