CL-1: Field-tested Learning Assessment Guide (FLAG): CATs: 'Creating Measures' Tasks

Mathematical Thinking CATs || Fault Finding and Fixing || Plausible Estimation
Creating Measures || Convincing and Proving || Reasoning from Evidence

Classroom Assessment Techniques
'Creating Measures' Tasks

(Screen 2 of 4)

Description
"Creating Measures" tasks consist of a series of questions that require students formally and quantitatively to define a measure of some concept. The concepts are ones of which students are intuitively aware, but which they have probably never attempted to describe mathematically. For example, students are asked to consider how they would define and quantify such concepts as "squareness," "sharpness," or "compactness." Usually, there are no formally correct and universally agreed-upon answers to such questions, but some definitions are clearly more useful than others. Students are required to not only come up with a measure of the concept, but also to evaluate how well that measure works as a mathematical description of a concept.

To offer one example, let us consider the problem of finding a measure for the "squareness" of a rectangle. One candidate might be: "the difference between the longest and shortest sides." This may seem sensible at first glance as it gives a measure of zero for squares and a larger measure as the difference between the two dimensions of the rectangle increases. One problem is, however, that the measure depends on the units used for measurement. A second related problem is that two mathematically similar rectangles will give a different value for the measure. Clearly a measure that does not depend upon the dimensions of the object would be better, such as "longest side/shortest side."

Example of "Creating Measures" Task

"Steep-ness" of Staircases

This problem gives you the chance to

criticize a given measure for the concept of 'steep-ness;'
invent your own ways of measuring this concept; and
examine the advantages and disadvantages of different methods.

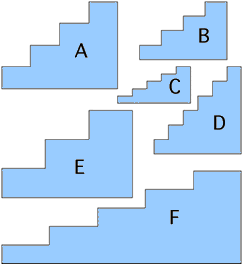
Image showing 6 different sets of stairs with different sized steps.

Warm-up

Without measuring anything, put the above staircases in order of steep-ness.

Someone has suggested that a good measure of 'steep-ness' is to calculate the difference Height of step - length of step for each staircase. Use this definition to put the staircases in order of steep-ness. Show all your work.
Using your results, give reasons why Height of step - length of step may not be a suitable measure for "steep-ness".
Invent a better way of measuring "steep-ness". Describe your method carefully.
Place the staircases in order of "steep-ness" using your method. Show all your work.
Do you think your measure is a good way of measuring "steep-ness"? Explain your reasoning carefully.
Describe a different way of measuring "steep-ness".
Compare the two methods you invented. Which is best? Why?

Thus "creating a measure" in most cases involves combining collections of measurements in new ways and considering the dimensionality of the result.

Assessment Purposes
There are three assessment purposes:

to see how well students are able to evaluate the usefulness of a quantitative measure for an intuitive concept;

to see how far students are able to define their own quantitative measure; and,

to see how far students are able to explore the utility of a measure in a context other than the one in which it was formulated.

Limitations
"Creating Measures" tasks are meant to measure the students' ability to "mathematize" a concept, or their ability to define a numerical measure of a concept, as well as evaluate the usefulness of that measure. This is important in that students can see that measures used to model phenomena in science are socially agreed-upon notions that exist primarily because of their usefulness. For most tasks, little mathematical technique is required and so these tasks do not assess algebraic techniques.