Suggestions for Use
Introducing 'Convincing and Proving' tasks for the first time
Many students will find these tasks unfamiliar since many have been required to provide proofs only for well-known results in geometry (which are often produced on demand after rote learning). Students are rarely asked to consider statements and evaluate their validity.
The first time you use these tasks, we suggest that you offer just one statement and allow students to discuss whether it is always, sometimes or never true, in small groups. For example, you can use the statement:
When you add two numbers, you get the same result as when you multiply them.
At first glance, most students would probably say that such a statement is 'false' or only true when the numbers are both zero or both two. It is worth pausing at this stage and asking whether there are any more cases. If no suggestions are forthcoming, or students appear quite confident that there aren't any more, suggest they try 3/2 and 3. They are often surprised by this example. Now ask them to try to find every case where the statement is true.
After a while, you might like to display the following pairs of numbers that result in a true statement and ask students for conjectures on a general rule.
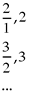
Some students may suggest continuing the pattern and trying
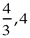
or even 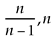
They may like to try checking other special cases (possibly containing decimals or negative numbers) or using algebra. From this, you can ask the students if they feel they have a proof that this set of answers is the set of all answers that work. If it is not, then ask the students what to do and allow them time to discuss this issue. They should realize that there may be many more answers which they haven't yet thought about.
Finally a 'proof' may be established:
This statement is sometimes true.
Proof:
Suppose one number is x and one number is y.
The statement says that: x + y = xy
This is true if and only if y = x/(x - 1)
So the statement works for any pair of numbers: (x, x/(x - 1))
It does not work if this condition does not hold.
Try to get students to explain why this proof is better than the previous line of argument.
Following this introduction, the students should be ready for more 'Convincing and Proving' tasks, which appear at the end of this document.
Providing guidance as students work on 'Convincing and Proving' tasks
Whether your students work in groups or individually, many will ask for guidance while doing the tasks. The amount of guidance that students need should decline as they become familiar with this type of problem. Early in class, you are likely to provide guidance by being a critical audience for their explanations and arguments. Later, if your primary goal is to encouragestudents to struggle with solving the problems on their own (and learn that they can be effective mathematical thinkers), you may choose to provide very little assistance.
Reporting out of individual or group work
If you decide to come together as a large group to discuss what students came up with (or report out), it is again helpful to decide the degree to which you will participate in these discussions, which will depend upon your goals for the session. For instance, you can facilitate the students' discussion, having them defend their ideas and write their ideas on the board, while adding almost none of your own. This discussion is the whole essence of convincing and proving; in fact, your role in this situation could be to provoke critical discussions of different solutions. At some point, you might want to review the session, focusing on the quality of different explanations, some techniques for testing mathematical conjectures, the characteristics of different sorts of 'non-proofs', or identifying different sorts of proof.
Formal and informal use of 'Convincing and Proving' tasks
These tasks can be used formally or informally. In formal assessment (where you grade the assignment as an examination), do not intervene except where specified. Even modest interventions - reinterpreting instructions, suggesting ways to begin, offering prompts when students appear to be stuck - have the potential to alter the task for the student significantly.
In informal assessment (an exercise, graded or non-graded), you may want to be less rigid in giving the students help. Under these circumstances, you may reasonably decide to do some coaching, talk with students as they work on the task, or pose questions when they seem to get stuck. In these instances you may be using the tasks for informal assessments-observing what strategies students favor, what kinds of questions they ask, what they seem to understand and what they are struggling with, and what kinds of prompts get them unstuck. This can be extremely useful information in helping you make ongoing instructional and assessment decisions. However, as students have more experiences with these kinds of tasks, the amount of coaching you do should decline and students should rely less on this kind of assistance.
Group work versus individual work
The communicative nature of "Convincing and Proving" tasks makes for great group discussions. Students can compare opinions and discuss the qualities of their various explanations. This may help them to refine their arguments. The CL-1 Collaborative Learning site can provide instructions on how to use group work effectively within the classroom. However, individual work may give you more clues as to each student's sophistication with this type of problem.
Presumed background knowledge
Most "Convincing and Proving" tasks do require some background in algebra, which provides students a way to expressing generality. Many of the explanations may be attempted initially without recourse to algebra, since examples and counterexamples are sought. Eventually, however, the student will want to know if the result always works, and in such cases the need for algebra becomes apparent to the student. Some basic knowledge of geometry will also be needed for some problems.
Step-by-Step Instructions
- Prepare by reading through the "Convincing and Proving" tasks on your own and coming up with your own solutions.
- Hand out copies of the task to students, either working individually or in groups. You may like to use the introduction above under "Suggestions for use."
- State the your goals for the "Convincing and Proving" task, emphasizing that students should try to find examples or counter examples, and write convincing explanations or reasons as to why they believe a statement to be always, sometimes, or never true. For the second set of tasks, they will need to identify flaws in someone else's reasoning.
- Walk around and listen to students as they discuss and work through the problems, providing guidance as necessary.
- Have students present their solutions, either in written or verbal form.
Tell me more about this technique:
Mathematical Thinking CATs || Fault Finding and Fixing || Plausible Estimation
Creating Measures || Convincing and Proving ||
Reasoning from Evidence

